¿Cómo se calcula la resonancia en un circuito RLC?

¿Alguna vez te has preguntado cómo se calcula la resonancia en un circuito RLC? Comprender los principios detrás de este cálculo puede ser crucial para los ingenieros eléctricos y técnicos.

En este artículo, te guiaremos a través del proceso paso a paso, utilizando un lenguaje claro y conciso para explicar conceptos como impedancia, reactancia, frecuencia de resonancia, inductancia, capacitancia y más.

Al final de este artículo, tendrás un sólido entendimiento de cómo calcular la resonancia en un circuito RLC.

¡Así que vamos a sumergirnos!

Breve descripción de los circuitos RLC

Los circuitos RLC son circuitos eléctricos que consisten en una resistencia (R), una bobina (L) y un condensador (C). Estos circuitos son ampliamente utilizados en electrónica y telecomunicaciones debido a sus propiedades y aplicaciones en el análisis de señales.

La resistencia R en el circuito RLC representa la oposición al flujo de corriente eléctrica. La bobina L almacena energía en forma de campo magnético cuando fluye corriente a través de ella. El condensador C almacena energía en forma de campo eléctrico.

Un circuito RLC es una combinación de resistores, inductores y capacitores que se conectan entre sí para crear un sistema eléctrico complejo. En este tipo de circuito, el impacto del inductor y el papel del capacitor son cruciales para comprender la resonancia.

La inductancia se refiere a la propiedad de un inductor que se opone a los cambios en el flujo de corriente. Se mide en henrios (H) y determina cuánta energía se puede almacenar en el campo magnético que rodea la bobina. Cuanto mayor sea la inductancia, más resistencia ofrece a los cambios en la corriente.

Por otro lado, la capacitancia se refiere a la capacidad de un capacitor para almacenar carga eléctrica. Se mide en faradios (F) y determina cuánta energía se puede almacenar como campo eléctrico entre sus placas. Cuanto mayor sea la capacitancia, más carga puede almacenar.

En un circuito RLC, ambos componentes desempeñan un papel importante en la determinación de la resonancia. La frecuencia de resonancia se calcula utilizando fórmulas que involucran tanto los valores de inductancia como los de capacitancia. Ajustando estos valores o añadiendo capacitores o inductores adicionales, los ingenieros pueden manipular las frecuencias de resonancia para aplicaciones específicas.

La frecuencia de resonancia se determina cuando la reactancia anula la impedancia. La reactancia se refiere a la oposición ofrecida por un inductor (reactancia inductiva) o un capacitor (reactancia capacitiva). La impedancia representa la oposición general ofrecida por todos los componentes combinados.

Comprender cómo funciona un circuito RLC requiere conocimiento de varios términos técnicos como impedancia, reactancia, frecuencia de resonancia, capacitancia, entre otros. Los ingenieros eléctricos utilizan un lenguaje preciso y cálculos al explicar estos conceptos sin jerga innecesaria ni ambigüedad.

Un enfoque estructurado implicaría presentar primero los circuitos RLC antes de adentrarse en los cálculos paso a paso involucrados en el cálculo de la resonancia.

Comprendiendo la resonancia en circuitos RLC

Para comprender la resonancia en los circuitos RLC, es importante entender el concepto de frecuencia de resonancia y su relación con los valores de los componentes del circuito.

La frecuencia de resonancia se refiere a la frecuencia en la cual un circuito RLC exhibe la máxima impedancia o la mínima reactancia.

El impacto de los valores de los componentes como la inductancia y la capacitancia en la frecuencia de resonancia puede calcularse utilizando fórmulas específicas, lo que permite un control preciso sobre el comportamiento del circuito.

Frecuencia de Resonancia Explicada

Para comprender la frecuencia de resonancia en un circuito RLC, debes saber que se calcula utilizando la fórmula f = 1 / (2π√(LC)). Esta fórmula te permite determinar la frecuencia a la cual la impedancia del circuito es puramente resistiva.

Aquí hay cuatro puntos clave que te ayudarán a profundizar tu comprensión:

• Aplicaciones de la frecuencia de resonancia: El cálculo de la frecuencia de resonancia es crucial para diseñar y analizar diversos sistemas eléctricos, como filtros, antenas y osciladores.

• Reactancia e impedancia: La reactancia se refiere a la oposición de un componente en un circuito eléctrico a la corriente alterna. La impedancia combina tanto la resistencia como la reactancia.

• Inductancia y capacitancia: Los inductores almacenan energía en campos magnéticos, mientras que los capacitores almacenan energía en campos eléctricos. Ambos afectan la frecuencia de resonancia de un circuito RLC.

• Proceso de cálculo paso a paso: Para calcular la frecuencia de resonancia, reúne los valores de la inductancia (L) y la capacitancia (C), luego sustitúyelos en la fórmula f = 1 / (2π√(LC)).

Comprender los cálculos de la frecuencia de resonancia permite a los ingenieros optimizar el rendimiento y la eficiencia en diversos dispositivos y sistemas electrónicos.

Impacto de los valores de los componentes

El impacto de diferentes valores de componentes en la frecuencia de resonancia puede ser significativo. En un circuito RLC, la frecuencia de resonancia está determinada por los valores de inductancia (L) y capacitancia (C). Al alterar estos valores, puedes ajustar la respuesta del circuito en su frecuencia de resonancia.

Veamos cómo afectan los diferentes valores de los componentes a la frecuencia de resonancia:

Componente	Efecto en la Frecuencia de Resonancia
Aumento en la Inductancia (L)	Disminuye la Frecuencia de Resonancia
Disminución en la Inductancia (L)	Aumenta la Frecuencia de Resonancia
Aumento en la Capacitancia (C)	Aumenta la Frecuencia de Resonancia
Disminución en la Capacitancia (C)	Disminuye la Frecuencia de Resonancia

Componentes clave de un circuito RLC

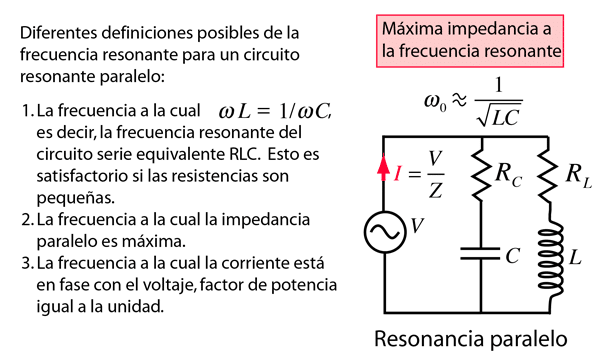
Al analizar un circuito RLC, es importante entender el papel del inductor. El inductor introduce reactancia, lo cual afecta la impedancia y la frecuencia de resonancia del circuito.

Además, la capacitancia en un circuito RLC tiene un impacto significativo en la resonancia. La reactancia del capacitor interactúa con la del inductor, creando una frecuencia de resonancia en la cual el circuito exhibe voltaje máximo y corriente mínima.

Por último, existe una relación entre la resistencia y la frecuencia en un circuito RLC. A medida que la frecuencia aumenta, la resistencia puede afectar significativamente el comportamiento del circuito al alterar su impedancia y características resonantes.

El papel del inductor en RLC

Comprender el papel del inductor en un circuito RLC es crucial para calcular la resonancia. El inductor juega un papel significativo en determinar el comportamiento del circuito a diferentes frecuencias. Aquí hay cuatro puntos clave a considerar:

• Impedancia: La impedancia del inductor, representada por ZL, depende de su reactancia y frecuencia.

• Respuesta en frecuencia: El inductor influye en la respuesta en frecuencia del circuito RLC debido a que su reactancia varía con la frecuencia.

• Frecuencia de resonancia: La inductancia determina la frecuencia de resonancia en la cual el circuito exhibe una impedancia máxima.

• Reactancia: La reactancia del inductor, XL, se opone a los cambios en el flujo de corriente y depende tanto de la frecuencia como de la inductancia.

Al comprender estos aspectos, puedes calcular con precisión la resonancia y diseñar circuitos que funcionen de manera óptima a frecuencias específicas.

Ten en cuenta estos factores al analizar o diseñar circuitos RLC para garantizar un funcionamiento eficiente.

Impacto del capacitor en la resonancia

Para calcular con precisión el impacto de un capacitor en la resonancia, deberás considerar su capacitancia y cómo influye en el comportamiento del circuito a diferentes frecuencias.

En un circuito RLC, el capacitor desempeña un papel crucial en el almacenamiento de energía y afecta la frecuencia de resonancia. La capacitancia del capacitor determina su capacidad para almacenar carga y, por lo tanto, afecta su reactancia a diferentes frecuencias.

En la resonancia, donde las reactancias del inductor y el capacitor se cancelan entre sí, el voltaje a través del capacitor se maximiza. Este efecto de voltaje se puede calcular utilizando fórmulas de impedancia que tienen en cuenta tanto la inductancia como la capacitancia.

Relación entre Resistencia y Frecuencia

Si aumentas la resistencia en un circuito, la frecuencia a la cual resuena disminuirá. Esto se debe a que la resistencia, junto con la inductancia y la capacitancia, juegan un papel crucial en la determinación de la frecuencia de resonancia de un circuito RLC.

Cuando aumenta la resistencia, se suma a la impedancia total del circuito, lo que provoca una disminución de la reactancia y, en última instancia, un cambio en la frecuencia de resonancia. El impacto de la resistencia en la resonancia se puede resumir de la siguiente manera:

• Un aumento de la resistencia conduce a una mayor impedancia.
• Una mayor impedancia reduce la reactancia.
• Una reducción de la reactancia altera la frecuencia de resonancia.
• En última instancia, aumentar la resistencia disminuye la frecuencia de resonancia.

Comprender esta relación entre la resistencia y la resonancia es vital para los ingenieros eléctricos y técnicos al diseñar circuitos o solucionar problemas relacionados con circuitos RLC. Manipulando cuidadosamente estos elementos, pueden optimizar el rendimiento del circuito y asegurarse de que la resonancia ocurra a las frecuencias deseadas.

El papel de la inductancia en el cálculo de la resonancia

La inductancia juega un papel importante en el cálculo de la resonancia en un circuito RLC. Para entender el efecto de la inductancia en la resonancia, es importante comprender primero el concepto de impedancia y reactancia.

La impedancia es la oposición total que un circuito ofrece a la corriente alterna, y está compuesta tanto por resistencia como por reactancia. La reactancia, por otro lado, se refiere a la oposición que surge debido a la capacitancia o inductancia.

En un circuito RLC, que consta de una resistencia (R), un capacitor (C) y un inductor (L), la frecuencia de resonancia puede determinarse considerando tanto las reactancias capacitivas como las inductivas. La frecuencia de resonancia ocurre cuando estas dos reactancias se cancelan entre sí, lo que resulta en una impedancia mínima.

Para calcular la resonancia en un circuito RLC, es necesario considerar las contribuciones individuales de cada componente. Los inductores tienen una propiedad llamada inductancia, que se opone a los cambios en el flujo de corriente. Esta propiedad afecta la magnitud y el ángulo de fase de la corriente que fluye a través de ellos.

El papel de un inductor en el cálculo de la resonancia implica determinar su reactancia en diferentes frecuencias utilizando la fórmula Xl=2πfL, donde Xl representa la reactancia del inductor, f es la frecuencia y L denota su valor de inductancia. Al encontrar este valor para diferentes frecuencias y compararlo con las reactancias de otros componentes, como la reactancia del capacitor Xc=1/2πfC, se puede determinar su efecto combinado en la impedancia en cada frecuencia.

El papel de la capacitancia en el cálculo de la resonancia

Ahora que hemos entendido el papel de la inductancia en el cálculo de la resonancia, vamos a explorar el papel de la capacitancia en este proceso.

La capacitancia juega un papel crucial en la determinación de la frecuencia resonante de un circuito RLC. Cuando se agrega un capacitor a un circuito RLC, introduce reactancia, que es la oposición al flujo de corriente alterna causada por la capacitancia. La reactancia causada por la capacitancia es inversamente proporcional a la frecuencia y directamente proporcional al valor de la capacitancia.

Aquí hay algunos puntos clave sobre el efecto de la capacitancia en la resonancia:

• La capacitancia afecta la impedancia de un circuito RLC en diferentes frecuencias.
• Valores más altos de capacitancia resultan en reactancias más bajas y, por lo tanto, en impedancias más bajas a frecuencias más altas.
• Valores más bajos de capacitancia conducen a reactancias más altas y, consecuentemente, a impedancias más altas a frecuencias más bajas.
• La presencia de capacitancia altera la frecuencia resonante y puede desplazarla dependiendo de su valor.

El papel de la capacitancia en el cálculo de la frecuencia de resonancia implica considerar su impacto en la reactancia. Al calcular la reactancia capacitiva utilizando fórmulas específicas relacionadas con la frecuencia y la capacitancia, los ingenieros pueden determinar cómo los cambios en la capacitancia afectarán la resonancia.

El papel de la resistencia en el cálculo de la resonancia

Al considerar el papel de la resistencia en el cálculo de la resonancia, es importante entender su impacto en la frecuencia resonante de un circuito RLC. La resistencia afecta tanto la impedancia como la reactancia de un circuito, alterando el comportamiento general y las características de la resonancia.

Resistencia y frecuencia de resonancia

Para calcular la resonancia en un circuito RLC, deberás tener en cuenta la resistencia y la frecuencia de resonancia. La resistencia juega un papel crucial en la determinación del comportamiento del circuito en resonancia. En la resonancia, la impedancia del circuito es puramente resistiva, lo que significa que es igual al valor de la resistencia. Esto permite la transferencia máxima de potencia entre la fuente y el circuito.

Por otro lado, si la resistencia se desvía de su valor óptimo, puede afectar tanto la amplitud como el desfase de corriente o voltaje en componentes como inductores y capacitores.

Para asegurar un cálculo preciso de la resonancia, es importante tener en cuenta no solo el componente resistivo, sino también otros factores como la reactancia, la inductancia, la capacitancia y sus respectivos valores dentro del circuito.

• La resistencia determina la transferencia de potencia en resonancia.
• Las desviaciones del valor óptimo de resistencia afectan la amplitud y el desfase.
• La reactancia, inductancia y capacitancia contribuyen a la impedancia general.
• El cálculo preciso requiere considerar todos los valores de los componentes.

Impacto de la Resistencia

La resistencia en un circuito RLC afecta tanto la amplitud como el desplazamiento de fase de la corriente o el voltaje a través de los componentes. En un circuito RLC resonante, donde la reactancia del inductor y el capacitor se cancelan entre sí, la resistencia juega un papel crucial.

Determina la disipación de potencia en el circuito, lo que puede resultar en pérdida de energía debido al calor generado por elementos resistivos. Una resistencia más alta conduce a una mayor disipación de potencia y puede limitar la eficiencia general del circuito.

Además, la resistencia también afecta el ancho de banda de la resonancia. Una resistencia más alta ampliará el ancho de banda, lo que resulta en un rango más amplio de frecuencias que se pueden transmitir o recibir de manera efectiva.

Por lo tanto, es esencial considerar la resistencia al calcular la resonancia en un circuito RLC para garantizar un rendimiento óptimo y minimizar las pérdidas de potencia.

Fórmulas para calcular la frecuencia de resonancia

Puedes calcular la frecuencia de resonancia en un circuito RLC utilizando fórmulas específicas. La frecuencia de resonancia, representada por fr, es la frecuencia en la cual la impedancia del circuito es puramente resistiva y alcanza su valor mínimo.

Aquí hay algunos puntos clave a considerar al calcular la frecuencia de resonancia:

• Fórmula de la Frecuencia de Resonancia: La fórmula para calcular la frecuencia de resonancia en un circuito RLC está dada por fr = 1 / (2π√(L*C)), donde fr representa la frecuencia de resonancia, L denota la inductancia y C representa la capacitancia.

• Valores de Inductancia y Capacitancia: Para calcular con precisión la frecuencia de resonancia, necesitas conocer los valores de inductancia (L) y capacitancia (C) presentes en tu circuito RLC. Estos valores se pueden obtener de diagramas de circuitos o midiendo con instrumentos apropiados.

• Cálculo de Reactancia: La reactancia se refiere a la oposición que un componente ofrece al flujo de corriente alterna. En un circuito RLC, tanto los inductores como los capacitores tienen reactancias. Al calcular sus reactancias individuales a diferentes frecuencias, puedes determinar cuándo sus reactancias combinadas se cancelan entre sí en la resonancia.

• Aplicaciones Prácticas: Comprender cómo calcular la frecuencia de resonancia es crucial para muchas aplicaciones prácticas, como diseñar filtros, sintonizar receptores de radio u optimizar la transferencia de energía en sistemas eléctricos.

Cálculo paso a paso de la frecuencia de resonancia

Sigue estos pasos para calcular con precisión la frecuencia de resonancia en un circuito RLC:

• Determina los valores de inductancia (L) y capacitancia (C). Estos valores se pueden obtener del diagrama del circuito o midiendo con instrumentos adecuados.

• Calcula la reactancia de ambos componentes. La reactancia es una medida de la oposición al flujo de corriente alterna y varía con la frecuencia. Para un inductor, la reactancia (XL) se calcula mediante la fórmula 2πfL, donde f es la frecuencia y L es el valor de la inductancia. Para un capacitor, la reactancia (XC) se calcula mediante la fórmula 1/(2πfC), donde C es el valor de la capacitancia.

• Determina qué componente tiene una reactancia más alta a una frecuencia dada comparando los valores de XL y XC.

• Si XL > XC, entonces ajusta la frecuencia hasta que XL = XC utilizando la ecuación de impedancia Z = √(R^2 + (XL - XC)^2), donde R representa la resistencia.

• Una vez que XL = XC, sustituye este valor en cualquiera de las ecuaciones: XL = 2πfL o XC = 1/(2πfC).

• Resuelve para f para encontrar la frecuencia de resonancia: f = 1/(2π√(LC)).

Siguiendo estos pasos de cálculo, puedes determinar con precisión la frecuencia de resonancia de un circuito RLC basado en sus valores de inductancia y capacitancia.

Esta información permite a los ingenieros eléctricos y técnicos diseñar circuitos que operan de manera óptima a frecuencias específicas para diversas aplicaciones, como filtros o sistemas de comunicación.

Factores que afectan la resonancia en circuitos RLC

Para determinar con precisión la frecuencia de resonancia en un circuito RLC, se deben considerar los valores de inductancia y capacitancia, así como otros factores que afectan la resonancia. La resonancia es una característica clave de los circuitos RLC, los cuales están compuestos por una resistencia (R), una bobina (L) y un capacitor (C). Cuando estos tres elementos se combinan, interactúan para crear propiedades eléctricas específicas que se pueden aprovechar para diversas aplicaciones.

Factores que afectan la resonancia en los circuitos RLC:

• Inductancia: El valor de la inductancia determina cuánta oposición hay a los cambios en el flujo de corriente dentro del circuito. Inductancias más altas resultan en frecuencias de resonancia más bajas.

• Capacitancia: De manera similar, el valor de la capacitancia afecta la reactancia del circuito y, por lo tanto, su frecuencia de resonancia. Capacitancias más altas conducen a frecuencias de resonancia más altas.

• Resistencia: El componente de resistencia disipa energía del circuito e influye en la nitidez de la resonancia. Resistencias más altas causan picos de resonancia más amplios.

• Impedancia: La impedancia representa la oposición general al flujo de corriente dentro de un circuito. Para lograr la máxima transferencia de energía en la resonancia, es esencial que haya una coincidencia de impedancia.

Para calcular la frecuencia de resonancia de un circuito RLC, deberás utilizar fórmulas que tengan en cuenta estos factores. La frecuencia de resonancia se puede determinar encontrando el punto en el que las reactancias debidas a los capacitores y las bobinas se cancelan entre sí, dando como resultado una reactancia neta de cero.

Aplicaciones e importancia del cálculo de resonancia en circuitos RLC

Comprender las aplicaciones y la importancia de calcular la resonancia en circuitos RLC puede mejorar en gran medida el proceso de diseño y solución de problemas. El cálculo de la resonancia desempeña un papel crucial en diversas aplicaciones de ingeniería eléctrica, como el diseño de filtros, la sintonización de receptores de radio y el análisis de sistemas de energía.

Una aplicación importante del cálculo de la resonancia se encuentra en el diseño de filtros. Al determinar la frecuencia de resonancia de un circuito RLC, los ingenieros pueden seleccionar con precisión los valores apropiados para componentes como inductores y capacitores para lograr las características de filtrado deseadas. Esto les permite bloquear o pasar eficientemente ciertas frecuencias, lo que conduce a una mejor calidad de señal y reducción de ruido.

El cálculo de la resonancia también es esencial en la sintonización de receptores de radio. Al ajustar la capacitancia o inductancia en un circuito RLC, los ingenieros pueden sintonizar con precisión un receptor para que resuene en un rango de frecuencia específico. Esto permite una recepción y amplificación óptimas de las señales deseadas, al tiempo que se minimiza la interferencia de otras frecuencias.

En el análisis de sistemas de energía, el cálculo de la resonancia ayuda a identificar posibles problemas que pueden surgir debido a las interacciones entre diferentes componentes. Cuando la frecuencia natural de un circuito RLC coincide con perturbaciones externas o armónicos generados por otros equipos, puede resultar en una amplificación excesiva de voltaje o corriente. Al calcular los puntos de resonancia, los ingenieros pueden tomar las medidas necesarias para mitigar estos efectos y garantizar un funcionamiento estable de los sistemas de energía.

Preguntas frecuentes

¿Cómo afecta la resonancia en un circuito RLC al factor de potencia?

La resonancia en un circuito RLC puede tener un impacto significativo en el factor de potencia. Cuando el circuito está en resonancia, los componentes reactivos se cancelan entre sí, resultando en una carga puramente resistiva. Esto conduce a un factor de potencia de unidad, lo que significa que toda la energía suministrada por la fuente se utiliza de manera efectiva.

Sin embargo, es importante tener en cuenta que la resonancia también puede causar corrientes elevadas y magnificación de voltaje, lo que puede resultar en sobrecalentamiento o daño a los componentes. Por lo tanto, aunque la resonancia tiene ventajas en términos de mejora del factor de potencia, también tiene posibles desventajas que deben ser consideradas.

¿Cuáles son algunas aplicaciones prácticas de la resonancia en circuitos RLC?

En aplicaciones prácticas de resonancia en circuitos RLC, es importante entender las limitaciones.

La resonancia se puede utilizar en varios dispositivos electrónicos como filtros, amplificadores y osciladores para mejorar el rendimiento. Ajustando los valores de inductancia y capacitancia, los ingenieros pueden lograr una frecuencia de resonancia que maximice el voltaje o la corriente.

Sin embargo, la resonancia también tiene sus desventajas. Puede causar calentamiento excesivo debido al aumento de la impedancia y la reactancia. Por lo tanto, se debe prestar atención cuidadosa para garantizar un funcionamiento seguro y prevenir daños a los componentes.

¿Puede ocurrir resonancia en un circuito RLC sin la presencia de una fuente de voltaje externa?

La resonancia en un circuito RLC puede ocurrir sin la presencia de una fuente de voltaje externa, pero existen limitaciones.

En diferentes configuraciones de circuito, como en serie o en paralelo, la resonancia se puede lograr ajustando los valores de la inductancia y la capacitancia para que coincidan con la frecuencia de resonancia natural del circuito.

La frecuencia de resonancia se determina mediante la fórmula 1/(2π√(LC)), donde L es la inductancia y C es la capacitancia.

¿Cómo afecta el factor de calidad de un circuito RLC a sus características de resonancia?

El factor de calidad de un circuito RLC tiene un impacto significativo en sus características de resonancia. Determina la relación entre la energía almacenada y disipada en el circuito, afectando directamente su amortiguamiento.

Un factor de calidad alto indica un amortiguamiento bajo, permitiendo que el circuito resuene fuertemente en su frecuencia de resonancia. Por el contrario, un factor de calidad bajo resulta en un amortiguamiento alto y una resonancia más débil.

Para calcular el factor de calidad, es necesario considerar factores como la impedancia, reactancia, inductancia y capacitancia dentro del circuito.

¿Existen Limitaciones o Desventajas al Usar Resonancia en Circuitos RLC para Aplicaciones Específicas?

Al considerar las limitaciones y desventajas de utilizar la resonancia en circuitos RLC para aplicaciones específicas, es importante tener en cuenta que una limitación potencial podría ser la dependencia de una fuente de voltaje externa. Esto significa que si la fuente externa falla o no está disponible, no se puede lograr el efecto de resonancia.

Además, ciertas aplicaciones pueden requerir valores de reactancia específicos que no son fácilmente alcanzables con inductores y condensadores estándar. Esto también podría limitar la efectividad de utilizar la resonancia en esos casos.

Conclusión

En conclusión, la resonancia en un circuito RLC se puede calcular utilizando fórmulas y principios específicos.

Los componentes clave de un circuito RLC, como la inductancia y la capacitancia, desempeñan roles cruciales en la determinación de la frecuencia de resonancia.

Al comprender las fórmulas para calcular la frecuencia de resonancia y seguir un proceso de cálculo paso a paso, los ingenieros eléctricos y técnicos pueden determinar con precisión la frecuencia de resonancia de un circuito RLC.

Este conocimiento es esencial para diversas aplicaciones en ingeniería eléctrica, ya que permite el diseño eficiente y la optimización de circuitos.